Opamps

Posted on Jun 11, 2022

Opamp attributes

Inverting input v1, non-inverting input v2: $$v_2-v_1=0$$ $$v_o=A(v_2-v_1)$$
Ideal characteristics:
- A -> infty
- Input currents -> 0
- Rin -> intfy
- Rout -> 0
- Slewrate -> infty
- Bandwidth -> intfy

Inverting amplifier

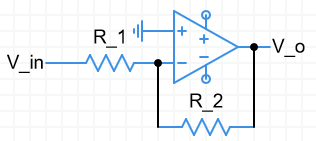
Inverting amplifier

$$A=\frac{v_o}{v_{in}}=\frac{-R_2}{R_1}$$

Non-inverting amplifier

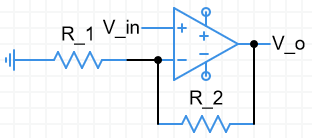
Non-inverting amplifier

$$A=\frac{v_o}{v_{in}}=1+\frac{R_2}{R_1}$$

Integrator

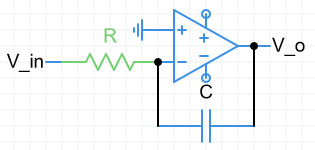
Integrator

$$v_o=\frac{-1}{RC}\int v_{in}dt$$

Differentiator

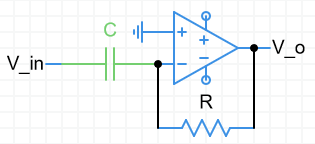
Differentiator

Note: In this form, the circuit is not stabe, as high frequency noise can send it into oscillation $$v_o=-RC\frac{dv_{in}}{dt}$$

Inverting summer

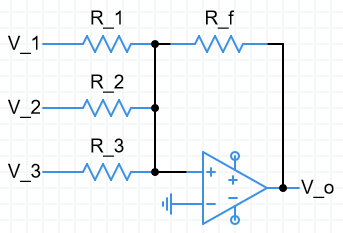
Inverting summer

$$v_o=-[v_1(\frac{R_f}{R_1})+v_2(\frac{R_f}{R_2})…]$$

Buffer

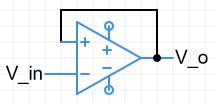
Buffer

$$v_o=v_{in}$$

Low pass filter

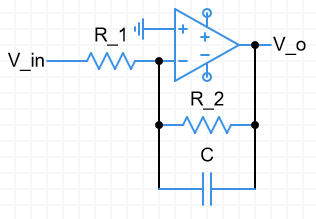
Low pass

$$A(jω)=\frac{-Z_2}{Z_1}=\frac{-R_2/R_1}{1+jωCR_2}$$

Limits tests $$@ω=0: A(jω)=\frac{-R_2}{R_1},@ω=\infty: A(jω)=0$$
Cutoff $$ω_c=\frac{1}{CR_2}, f_c=\frac{1}{2\pi CR_2}$$

High pass filter

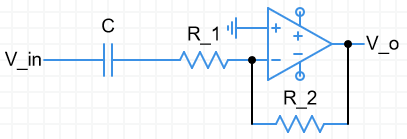
High pass

$$A(jω)=\frac{-Z_2}{Z_1}=\frac{jωCR_2}{1+jωCR_1}$$

Limits tests $$@ω=0: A(jω)=0,@ω=\infty: A(jω)=\frac{-R_2}{R_1}$$
Cutoff $$ω_c=\frac{1}{CR_1}, f_c=\frac{1}{2\pi CR_1}$$

Band pass filter

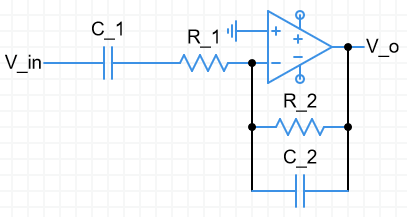
Band pass

$$A(jω)=\frac{-Z_2}{Z_1}=\frac{jωCR_2}{(1+jωCR_1)(1+jωCR_2)}$$

Limits tests & cutoff harder to determine (2nd order filter)