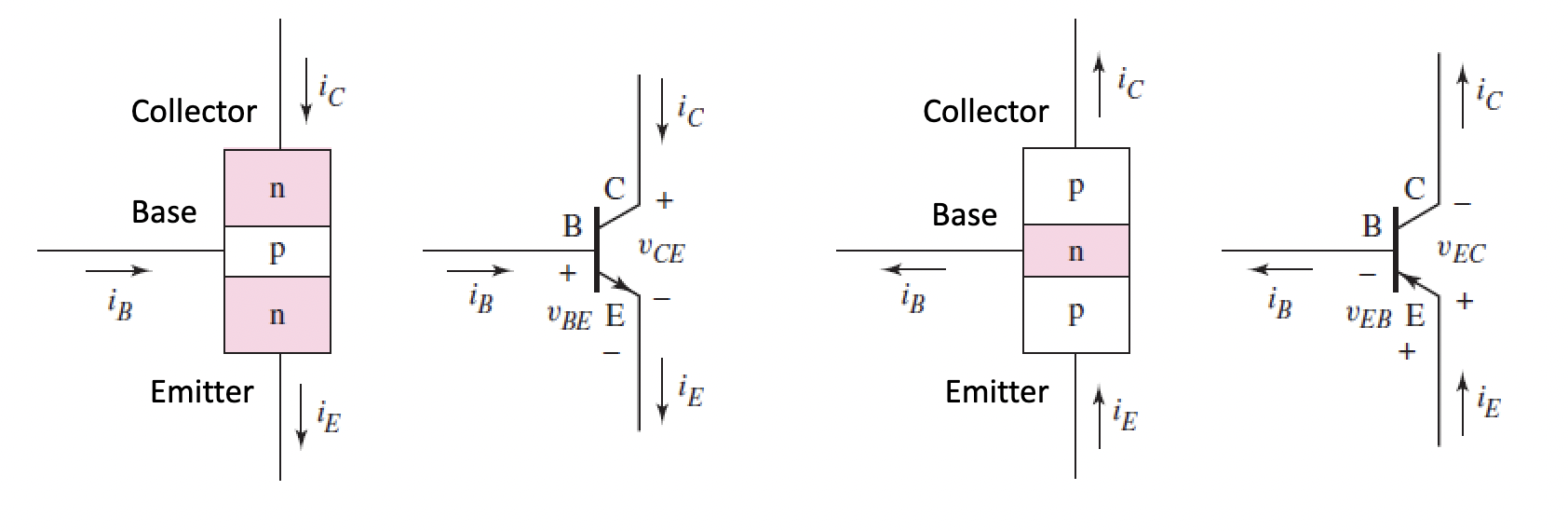
BJTs

• Analogue design focuses on the forward-active mode of BJTs (B-E forward biased, C-B reverse biased)
• β is the common-emitter current gain, usually ~150 $$β=\frac{i_C}{i_B}, i_C=βi_B$$ $$i_E=i_B+i_C$$
• α is the common-base current gain $$α=\frac{β}{β+1}, β=\frac{α}{1-α}$$ $$i_E=\frac{i_C}{α}$$ For a large β: $$α\approx 1$$
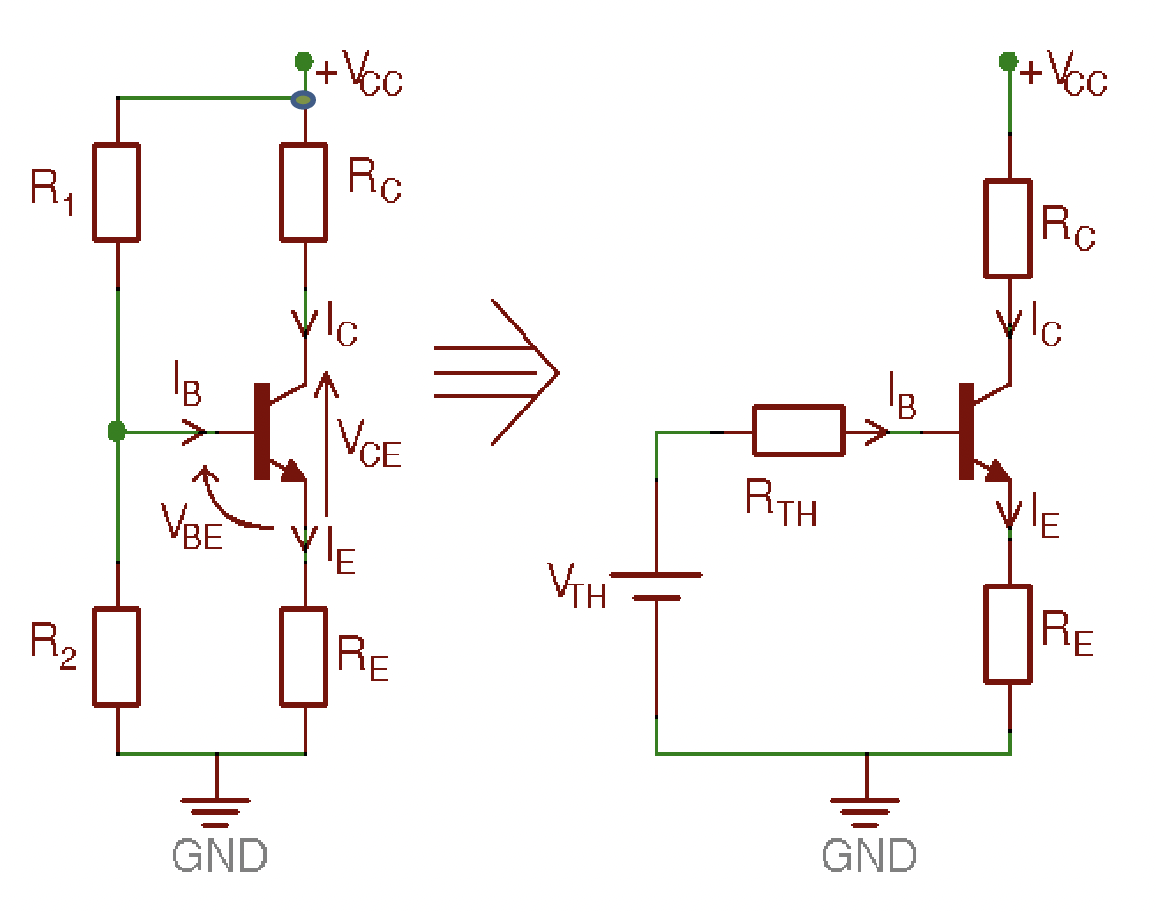
• For a BJT (npn and pnp respectively), we take: $$v_{BE}=0.7v, v_{EB}=0.7v$$

DC analysis

• We want to set up a Q-point (quiescent) to a certain specification, we do this by setting resistor values

• Consider: $$R_{Th}=R_1||R_2, V_{Th}=V_{CC}\frac{R_2}{R_1+R_2}$$ If split power: $$V_{Th}=(V_{CC}-V_{EE})\frac{R_2}{R_1+R_2}$$
• Using this Thévenin equivalent circuit: $$I_B=\frac{V_{Th}-V_{BE}}{R_{Th}+(1+β)R_E}$$
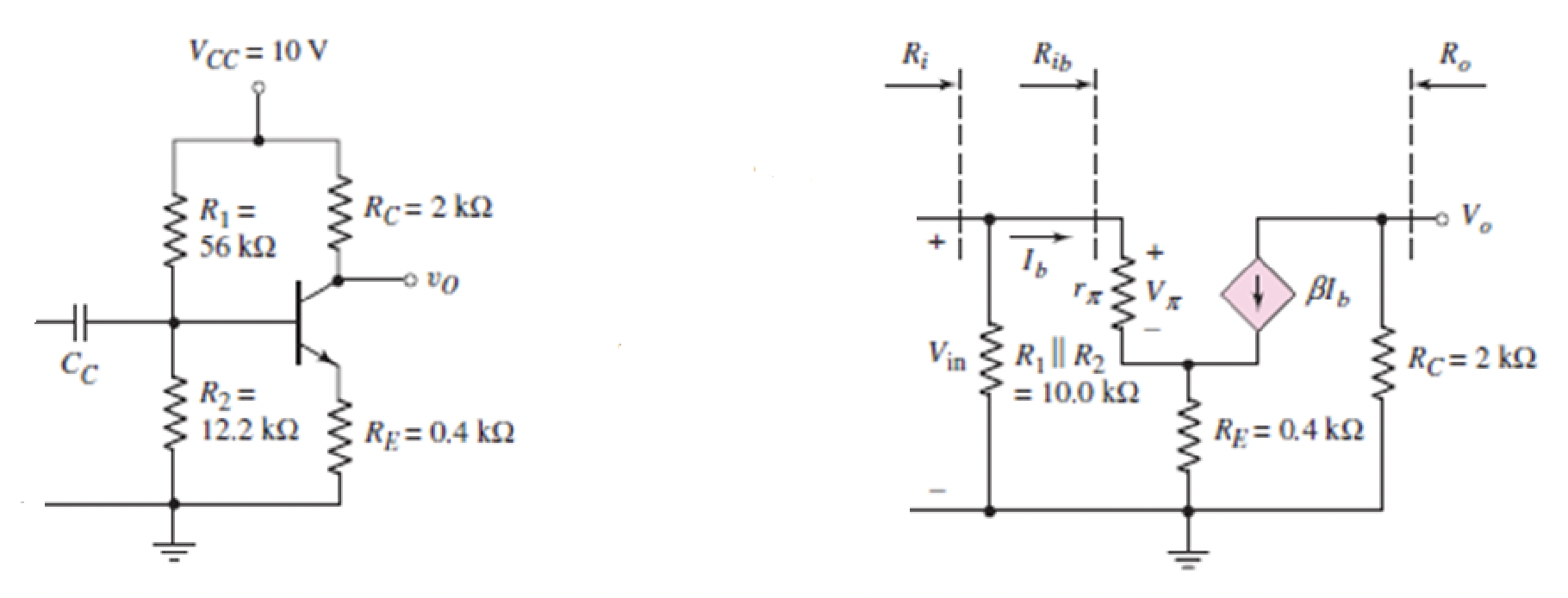
• Stabilising I_C by design: we can choose a ‘small’ R_Th i.e. $$R_{Th}=\frac{βR_E}{10}$$ This lets us simplify: $$I_C\approx I_E$$

AC analysis

• Voltage form of the above: $$βI_b\implies g_mV_{be}$$
• To transform a circuit for AC analysis:
  • Replace capacitors with short circuits
  • Replace DC volt sources with shorts to ground
  • Replace the BJS with the hybrid π model shown above
• V_T is the thermal voltage (assume =25mV), g_m is the transconductance of the BJT $$g_m=\frac{I_{CQ}}{V_T}=40I_{CQ}$$
• Internal resistance $$r_π=\frac{βV_T}{I_{CQ}}=\frac{β}{g_m}$$
• Input impedence @ base $$R_{ib}=\frac{V_{in}}{i_b}=r_π+R_E(1+β)$$ Impedence @ ri $$R_i=R_{ib}||R_1||R_2=(r_π+R_E(1+β))||R_{Th}$$
• Voltage in $$V_{in}=i_bR_{ib}=i_b(r_π+R_E(1+β))$$ Voltage out $$V_o=-βI_bR_C$$ Therefore: Voltage gain: $$A_v=\frac{V_o}{V_{in}}=\frac{-βI_bR_C}{i_b(r_π+R_E(1+β))}=\frac{-βR_C}{R_E(1+β)}$$ For large β: $$A_v=\frac{-R_C}{R_E}$$ Note: negative sign implies 180° phase shift (inverting)